Tutorial: Generating Newton Fractal for a simple function¶
Introduction to Fractal¶
A fractal is never ending pattern. Fractals are a type of mathematical shape that are infinitely complex. They are created by repeating a simple process over and over in an ongoing feedback loop.
In essence, a Fractal is a pattern that repeats forever, and every part of the Fractal, regardless of how zoomed in, or zoomed out you are, it looks very similar to the whole image. A shape does not have to be exactly identical to be classified as a Fractal. Instead shapes that display inherent and repeating similarities are the main requirement for being classified as a Fractal. [Falconer1990]
Fractals are found all over nature, spanning a huge range of scales. We find the same patterns again and again, from the tiny branching of our blood vessels and neurons to the branching of trees, lightning bolts, snowflakes, river networks and even the clustering of galaxies. Regardless of scale, these patterns are all formed by repeating a simple branching process.
Fig: Fractal in nature, geometry, and algebra [Jasser]
For more background information on fractals: [FractalFoundation2009].
Newton Fractal¶
One way of generating fractals is using Newton-Raphson Method, also known as Newton Fractal. Newton fractals are fractals created in the plane of complex numbers. An iteration process with Newton’s method is started at each point on a grid in the complex plane, and a color is assigned to each point according to which of the roots of a given function the iteration converges to. [Sahari2006]
A generalisation of Newton’s iteration is:
where \(z \in \mathbb{C}\) represents any point in the plane, \(n \in \mathbb{N}\) represents the number of step, and \(f(z)\) is a polynomial or transcendental function.
For \(f(z) = z^3 - 1\), the iteration is:
Installing FractPy¶
Let us now see how to plot fractal for this function using FractPy, but first we need to install it. FractPy requires Python 3.6 or greater, so assuming you have it, to install FractPy:
On Mac OSX or linux open a terminal;
On Windows open the Command prompt or similar
and type:
$ python -m pip install fractpy
Using FractPy¶
Generating fractals in fractpy can be divided into 2 steps:
Creating a model
Generating the fractal
Creating a Model¶
A model represents the technique being used to generate the fractal,
so generating fractal from Newtons’ method would involve making a
model NewtonFractal which is a class of module fractpy.models,
and then passing the required function in the form str as an
argument during initialisation. The following code shows how to
make a NewtonFractal model for the above function:
>>> from fractpy.models import NewtonFractal
>>> model = NewtonFractal("x**3 - 1")
>>> model
### FractPy Model ###
Type: Newton Fractal
Function: x**3 - 1
Note
For complex values use I (upper case i) instead of commonly used
convention of i. For example: function
\(f(x) = (x - 1)(x + i)(x - i)\) would be passed as
"(x - 1)(x + I)(x - I)".
Generating Fractal¶
To generate the fractal all we have to do now is call the method plot,
and pass in the axes limits along with the desired resolution of the
image which returns a matplotlib.figure.Figure:
>>> xmin, xmax, ymin, ymax = -2, 2, -2, 2
>>> p = model.plot(xmin, xmax, ymin, ymax, (500, 500))
>>> p.show()
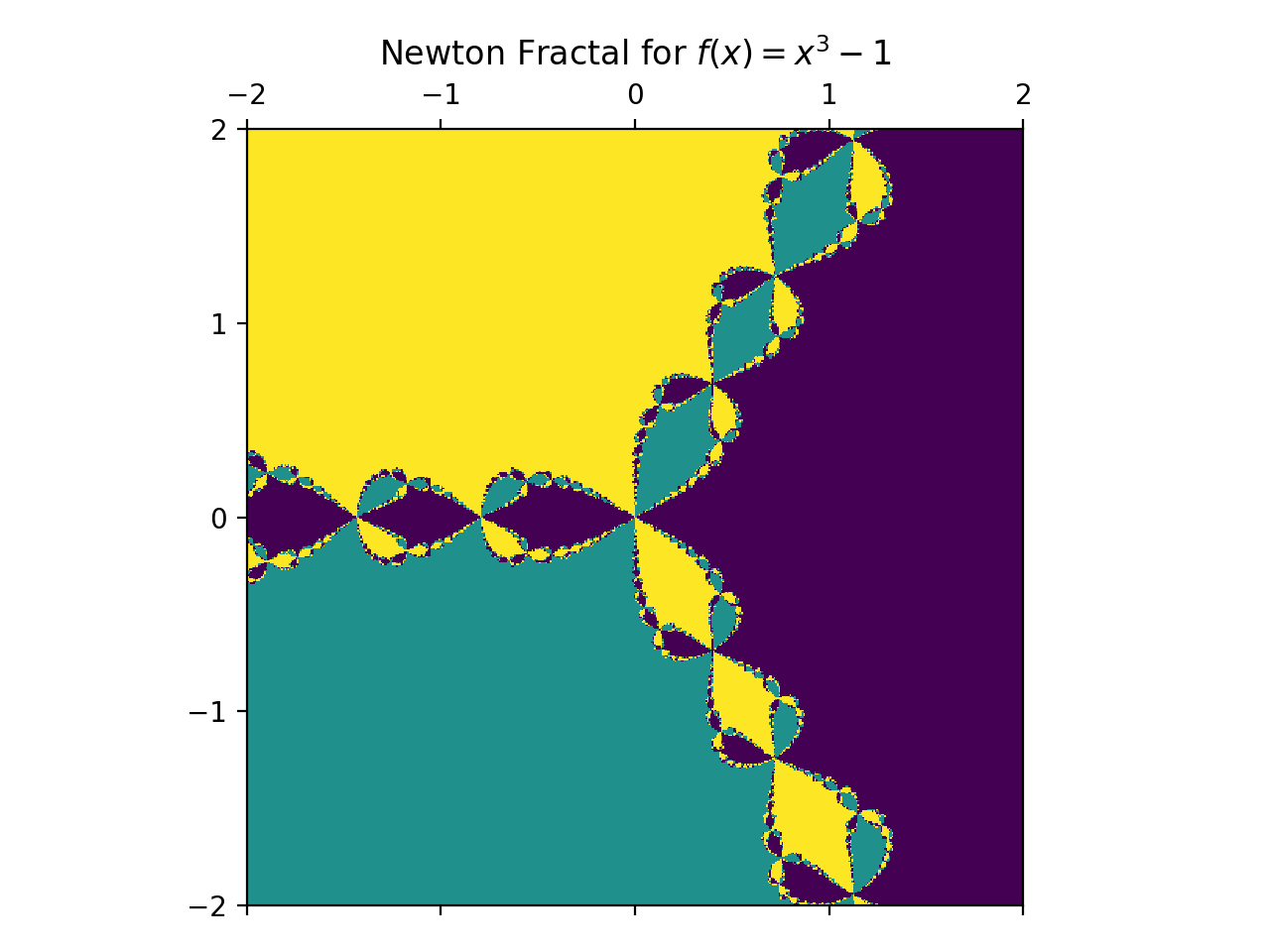
The above code will generate the Newton Fractal for \(x^3 - 1\), in the range -2 to 2 for both x-axis and y-axis, and the resolution of the image would be 500X500.
This creates the following plot:
Note
Generating fractal requires some heavy computation so it may take seconds, or minutes depending on the computing power of the system.